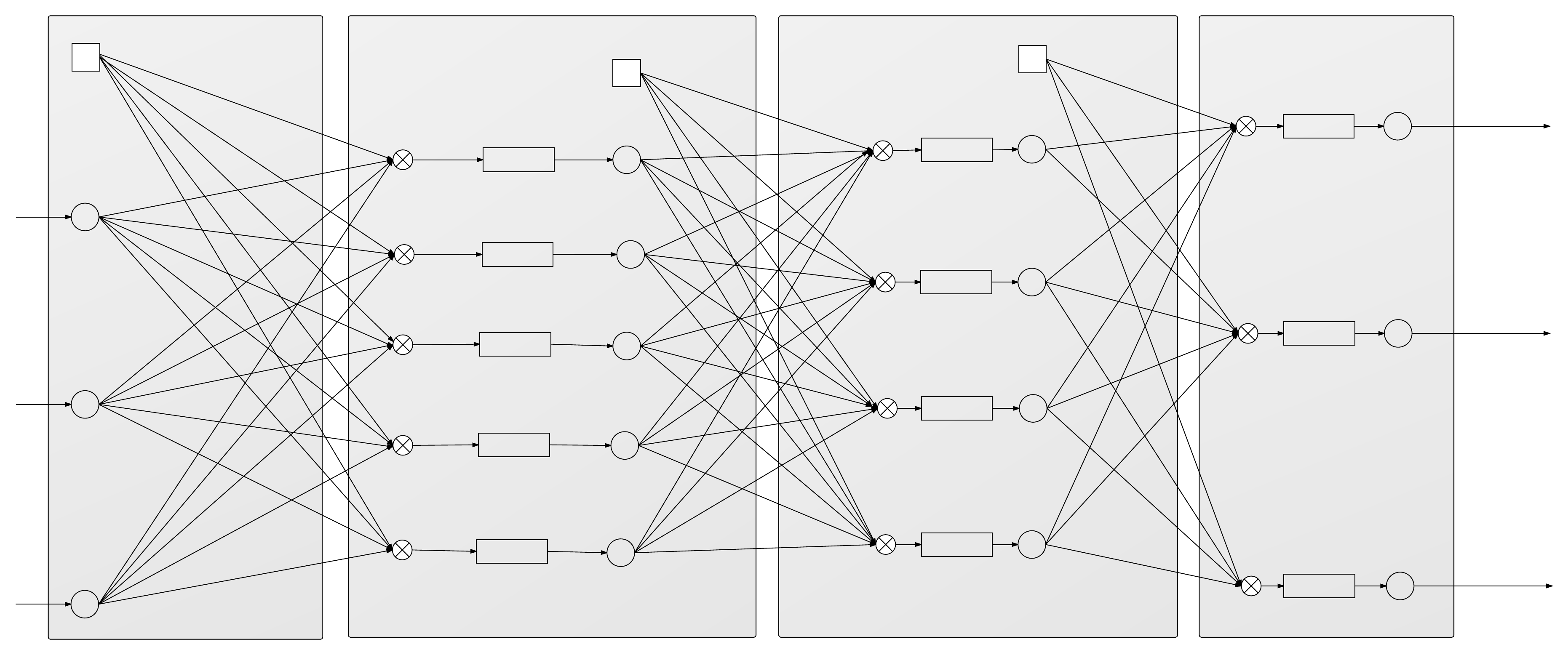
This demonstrates a neural network with both forward propagation and back propagation. Each network assumes one output variable but the variable can take many possible values.

\[ \]
| \( L \): | Number of layers (includes input and output layers), \( \hspace{2em} {\color{gray} l\in \left \{ 1,...,L \right \} } \) | |
| \( \Theta^{[l]} \): | Array of parameters (or “weights”) on layer \( l \), \( \hspace{2em} {\color{gray} \left\vert{ \Theta^{[l]} }\right\vert = \left\{ (u^{[l]}+1) \times u^{[l+1]} \right\} } \) | |
| \( \theta^{[l]}_{i,j} \): | Parameter value (or “weight”) of \( i \)'th observation and \( j \)'th input variable on layer \( l \). \( \; \) (Note: \(j = 0 \) indicates the bias term.) | |
| \( X \): | Array of input variables, \( \hspace{2em} {\color{gray} \left\vert{ X }\right\vert = \left\{ m \times n \right\} } \) | |
| \( x_{i,j} \): | Value of \( i \)'th observation of input variable \( j \) | |
| \( Y \): | Vector of output variable ("response","target") values, \( \hspace{2em} {\color{gray} \left\vert{ Y }\right\vert = \left\{ m \times 1 \right\} } \) | |
| \( y_{i} \): | Value of \( i \)'th observation of the output variable | |
| \( g(.) \): | The Activation Function. Typically, this is the logistic function or hyperbolic tangent. | |
| \( Z^{[l]} \): | Array of Transfer Function inputs with \( \Theta^{[l]} \) weights, \( \hspace{2em} {\color{gray} \left\vert{ Z^{[l]} }\right\vert = \left \{ m \times u^{[l]} \right \} } \) | |
| \( z^{[l]}_{i,m} \): | Value of \( i \)'th observation \( Z^{[l]} \) at \( m \)'th unit on layer \( l \) | |
| \( H^{[l]} \): | Array of Transfer Function outputs, \( \hspace{2em} \) \( {\color{gray} \left\vert{ Z^{[l]} }\right\vert = \left \{ m \times u^{[l]} \right \} } \) | |
| \( u^{[l]} \): | Size (i.e. the number of units) of layer \( l \). (Note: The input layer corresponds to \( l = 1 \).) | |
| \( A^{[l]} \): | Layer inputs, \( \hspace{2em} \) \( {\color{gray} \left\vert{ A^{[l]} }\right\vert = \left \{ m \times (u^{[l]} + 1) \right \} } \) | |
| \( m \): | Number of observations, \( \hspace{2em} {\color{gray} i\in \left \{ 1,...,m \right \} } \) | |
| \( n \): | Number of input variables ("features","inputs","predictors","independent variables"), \( \hspace{2em} {\color{gray} j\in \left \{ 1,...,n \right \} } \) |
\[ \]
\[ \]
The example data here is synthesized. Our output variable, \( Y \), is a binary-valued variable designated as either \( 0 \) or \( 1 \). The matrix \( X \) consists of m*n elements, \( x_{i,j} \) where \( i \in \{1,...,m\} \) and \( j \in \{1,...n\} \)
\[ \]
\[ X = \left[ x_{i,j} \right] = \left( \begin{array}{X} x_{1,1} & x_{1,2} & x_{1,3} \\ x_{2,1} & x_{2,2} & x_{2,3} \\ x_{3,1} & x_{3,2} & x_{3,3} \\ x_{4,1} & x_{4,2} & x_{4,3} \\ x_{5,1} & x_{5,2} & x_{5,3} \\ x_{6,1} & x_{6,2} & x_{6,3} \\ x_{7,1} & x_{7,2} & x_{7,3} \\ \end{array} \right), \hspace{1em} Y = \left[ y_{i} \right] = \left( \begin{array}{Y} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ y_{5} \\ y_{6} \\ y_{7} \\ \end{array} \right ) \]
\[ \]
\[ \color{gray} \left\vert{X}\right\vert = \left \{ m \times n \right \} ,\hspace{2em}\left\vert{Y}\right\vert = \left \{ m \times 1 \right \} \]
\[ \]
## Create simulated input-variable matrix, X
X <- matrix(c(1, 2, 15, 2, 16, 18, 19, 18, 20, 1, 20, 1, 1, 2, 1, 1, 17, 1,
18, 18, 19), ncol = 3)
show(X)
## [,1] [,2] [,3]
## [1,] 1 18 1
## [2,] 2 20 1
## [3,] 15 1 17
## [4,] 2 20 1
## [5,] 16 1 18
## [6,] 18 1 18
## [7,] 19 2 19
## Create simulated output-variable, Y
Y <- matrix(c(0, 0, 1, 0, 1, 1, 1), ncol = 1)
show(Y)
## [,1]
## [1,] 0
## [2,] 0
## [3,] 1
## [4,] 0
## [5,] 1
## [6,] 1
## [7,] 1
\[ \]
The input data matrix, \( X \), becomes \( A^{[1]} \) after a column of ones is appended to \( X \). The column of ones (i.e. the first column in the matrix \( A^{[1]} \) below) serves as a place holder for the bias term parameters, \( \theta_{0,j} \). The \( X \) values are also typically normalized. Below, when constructing the matrix “A1” in R, \( X \) is normalized by its maximum value.
\[ \]
\[ A^{[1]} = \left( \begin{array}{X1} 1 & x_{1,1} & x_{1,2} & x_{1,3} \\ 1 & x_{2,1} & x_{2,2} & x_{2,3} \\ 1 & x_{3,1} & x_{3,2} & x_{3,3} \\ 1 & x_{4,1} & x_{4,2} & x_{4,3} \\ 1 & x_{5,1} & x_{5,2} & x_{5,3} \\ 1 & x_{6,1} & x_{6,2} & x_{6,3} \\ 1 & x_{7,1} & x_{7,2} & x_{7,3} \\ \end{array} \right) = \left( \begin{array}{A1} a^{[1]}_{1,0} & a^{[1]}_{1,1} & a^{[1]}_{1,2} & a^{[1]}_{1,3} \\ a^{[1]}_{2,0} & a^{[1]}_{2,1} & a^{[1]}_{2,2} & a^{[1]}_{2,3} \\ a^{[1]}_{3,0} & a^{[1]}_{3,1} & a^{[1]}_{3,2} & a^{[1]}_{3,3} \\ a^{[1]}_{4,0} & a^{[1]}_{4,1} & a^{[1]}_{4,2} & a^{[1]}_{4,3} \\ a^{[1]}_{5,0} & a^{[1]}_{5,1} & a^{[1]}_{5,2} & a^{[1]}_{5,3} \\ a^{[1]}_{6,0} & a^{[1]}_{6,1} & a^{[1]}_{6,2} & a^{[1]}_{6,3} \\ a^{[1]}_{7,0} & a^{[1]}_{7,1} & a^{[1]}_{7,2} & a^{[1]}_{7,3} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{A^{[1]}}\right\vert = \left \{ m \times ( n + 1 ) \right \} = \left \{ m \times ( u^{[1]} + 1 ) \right \} \]
\[ \]
A1 <- cbind(matrix(rep(1, 7), ncol = 1), X/max(X))
show(A1)
## [,1] [,2] [,3] [,4]
## [1,] 1 0.05 0.90 0.05
## [2,] 1 0.10 1.00 0.05
## [3,] 1 0.75 0.05 0.85
## [4,] 1 0.10 1.00 0.05
## [5,] 1 0.80 0.05 0.90
## [6,] 1 0.90 0.05 0.90
## [7,] 1 0.95 0.10 0.95
\[ \]
If \( (u^{[l]}+1) \) is the number of input variables from layer \( l \) and \( u^{[l+1]} \) is the number of units on layer \( l+1 \) then the dimensions of the parameter matrix, \( \Theta^{[l]} \), will be \( \left \{ (u^{[l]} + 1 ) \times u^{[l+1]} \right \} \).
\[ \]
\[ \Theta^{[1]} = \left( \begin{array}{Theta1} \theta^{[1]}_{0,1} & \theta^{[1]}_{0,2} & \theta^{[1]}_{0,3} & \theta^{[1]}_{0,4} & \theta^{[1]}_{0,5} \\ \theta^{[1]}_{1,1} & \theta^{[1]}_{1,2} & \theta^{[1]}_{1,3} & \theta^{[1]}_{1,4} & \theta^{[1]}_{1,5} \\ \theta^{[1]}_{2,1} & \theta^{[1]}_{2,2} & \theta^{[1]}_{2,3} & \theta^{[1]}_{2,4} & \theta^{[1]}_{2,5} \\ \theta^{[1]}_{3,1} & \theta^{[1]}_{3,2} & \theta^{[1]}_{3,3} & \theta^{[1]}_{3,4} & \theta^{[1]}_{3,5} \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{\Theta^{[1]}}\right\vert = \left \{ (u^{[1]} + 1 ) \times u^{[2]} \right \} \]
\[ \]
Theta1 <- matrix(runif(20), ncol = 5)
show(Theta1)
## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.1987506 0.406701953 0.4548451 0.86704065 0.5271858
## [2,] 0.7996204 0.001358987 0.4038082 0.90927248 0.1011752
## [3,] 0.1972418 0.838248148 0.6475877 0.01935939 0.5511545
## [4,] 0.9103090 0.946985035 0.4091616 0.96117030 0.1045232
\[ \]
The Transfer Function, \( z=\theta_{0}+ \sum \theta_{j} x_{j} \), is calculated with the inner product of the variable matrix, \( A^{[1]} \), and the parameter matrix, \( \Theta^{[1]} \).
\[ \]
\[ Z^{[2]} = A^{[1]} \cdot \Theta^{[1]} = \left( \begin{array}{A1} a^{[1]}_{1,0} & a^{[1]}_{1,1} & a^{[1]}_{1,2} & a^{[1]}_{1,3} \\ a^{[1]}_{2,0} & a^{[1]}_{2,1} & a^{[1]}_{2,2} & a^{[1]}_{2,3} \\ a^{[1]}_{3,0} & a^{[1]}_{3,1} & a^{[1]}_{3,2} & a^{[1]}_{3,3} \\ a^{[1]}_{4,0} & a^{[1]}_{4,1} & a^{[1]}_{4,2} & a^{[1]}_{4,3} \\ a^{[1]}_{5,0} & a^{[1]}_{5,1} & a^{[1]}_{5,2} & a^{[1]}_{5,3} \\ a^{[1]}_{6,0} & a^{[1]}_{6,1} & a^{[1]}_{6,2} & a^{[1]}_{6,3} \\ a^{[1]}_{7,0} & a^{[1]}_{7,1} & a^{[1]}_{7,2} & a^{[1]}_{7,3} \\ \end{array} \right ) \cdot \left( \begin{array}{Theta1} \theta^{[1]}_{0,1} & \theta^{[1]}_{0,2} & \theta^{[1]}_{0,3} & \theta^{[1]}_{0,4} & \theta^{[1]}_{0,5} \\ \theta^{[1]}_{1,1} & \theta^{[1]}_{1,2} & \theta^{[1]}_{1,3} & \theta^{[1]}_{1,4} & \theta^{[1]}_{1,5} \\ \theta^{[1]}_{2,1} & \theta^{[1]}_{2,2} & \theta^{[1]}_{2,3} & \theta^{[1]}_{2,4} & \theta^{[1]}_{2,5} \\ \theta^{[1]}_{3,1} & \theta^{[1]}_{3,2} & \theta^{[1]}_{3,3} & \theta^{[1]}_{3,4} & \theta^{[1]}_{3,5} \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{Z^{[2]}}\right\vert = \left \{ m \times (u^{[1]}+1) \right \} \cdot \left \{ (u^{[1]} + 1 ) \times u^{[2]} \right \} \]
\[ \]
\[ Z^{[2]} = \left( \begin{array}{Z2} \theta^{[1]}_{0,1} a^{[1]}_{1,0} + \theta^{[1]}_{1,1} a^{[1]}_{1,1} + \theta^{[1]}_{2,1} a^{[1]}_{1,2} + \theta^{[1]}_{3,1} a^{[1]}_{1,3} & & \theta^{[1]}_{0,2} a^{[1]}_{1,0} + \theta^{[1]}_{1,2} a^{[1]}_{1,1} + \theta^{[1]}_{2,2} a^{[1]}_{1,2} + \theta^{[1]}_{3,2} a^{[1]}_{1,3} & & \theta^{[1]}_{0,3} a^{[1]}_{1,0} + \theta^{[1]}_{1,3} a^{[1]}_{1,1} + \theta^{[1]}_{2,3} a^{[1]}_{1,2} + \theta^{[1]}_{3,3} a^{[1]}_{1,3} & & \theta^{[1]}_{0,4} a^{[1]}_{1,0} + \theta^{[1]}_{1,4} a^{[1]}_{1,1} + \theta^{[1]}_{2,4} a^{[1]}_{1,2} + \theta^{[1]}_{3,4} a^{[1]}_{1,3} & & \theta^{[1]}_{0,5} a^{[1]}_{1,0} + \theta^{[1]}_{1,5} a^{[1]}_{1,1} + \theta^{[1]}_{2,5} a^{[1]}_{1,2} + \theta^{[1]}_{3,5} a^{[1]}_{1,3} \\ \theta^{[1]}_{0,1} a^{[1]}_{2,0} + \theta^{[1]}_{1,1} a^{[1]}_{2,1} + \theta^{[1]}_{2,1} a^{[1]}_{2,2} + \theta^{[1]}_{3,1} a^{[1]}_{2,3} & & \theta^{[1]}_{0,2} a^{[1]}_{2,0} + \theta^{[1]}_{1,2} a^{[1]}_{2,1} + \theta^{[1]}_{2,2} a^{[1]}_{2,2} + \theta^{[1]}_{3,2} a^{[1]}_{2,3} & & \theta^{[1]}_{0,3} a^{[1]}_{2,0} + \theta^{[1]}_{1,3} a^{[1]}_{2,1} + \theta^{[1]}_{2,3} a^{[1]}_{2,2} + \theta^{[1]}_{3,3} a^{[1]}_{2,3} & & \theta^{[1]}_{0,4} a^{[1]}_{2,0} + \theta^{[1]}_{1,4} a^{[1]}_{2,1} + \theta^{[1]}_{2,4} a^{[1]}_{2,2} + \theta^{[1]}_{3,4} a^{[1]}_{2,3} & & \theta^{[1]}_{0,5} a^{[1]}_{2,0} + \theta^{[1]}_{1,5} a^{[1]}_{2,1} + \theta^{[1]}_{2,5} a^{[1]}_{2,2} + \theta^{[1]}_{3,5} a^{[1]}_{2,3} \\ \theta^{[1]}_{0,1} a^{[1]}_{3,0} + \theta^{[1]}_{1,1} a^{[1]}_{3,1} + \theta^{[1]}_{2,1} a^{[1]}_{3,2} + \theta^{[1]}_{3,1} a^{[1]}_{3,3} & & \theta^{[1]}_{0,2} a^{[1]}_{3,0} + \theta^{[1]}_{1,2} a^{[1]}_{3,1} + \theta^{[1]}_{2,2} a^{[1]}_{3,2} + \theta^{[1]}_{3,2} a^{[1]}_{3,3} & & \theta^{[1]}_{0,3} a^{[1]}_{3,0} + \theta^{[1]}_{1,3} a^{[1]}_{3,1} + \theta^{[1]}_{2,3} a^{[1]}_{3,2} + \theta^{[1]}_{3,3} a^{[1]}_{3,3} & & \theta^{[1]}_{0,4} a^{[1]}_{3,0} + \theta^{[1]}_{1,4} a^{[1]}_{3,1} + \theta^{[1]}_{2,4} a^{[1]}_{3,2} + \theta^{[1]}_{3,4} a^{[1]}_{3,3} & & \theta^{[1]}_{0,5} a^{[1]}_{3,0} + \theta^{[1]}_{1,5} a^{[1]}_{3,1} + \theta^{[1]}_{2,5} a^{[1]}_{3,2} + \theta^{[1]}_{3,5} a^{[1]}_{3,3} \\ \theta^{[1]}_{0,1} a^{[1]}_{4,0} + \theta^{[1]}_{1,1} a^{[1]}_{4,1} + \theta^{[1]}_{2,1} a^{[1]}_{4,2} + \theta^{[1]}_{3,1} a^{[1]}_{4,3} & & \theta^{[1]}_{0,2} a^{[1]}_{4,0} + \theta^{[1]}_{1,2} a^{[1]}_{4,1} + \theta^{[1]}_{2,2} a^{[1]}_{4,2} + \theta^{[1]}_{3,2} a^{[1]}_{4,3} & & \theta^{[1]}_{0,3} a^{[1]}_{4,0} + \theta^{[1]}_{1,3} a^{[1]}_{4,1} + \theta^{[1]}_{2,3} a^{[1]}_{4,2} + \theta^{[1]}_{3,3} a^{[1]}_{4,3} & & \theta^{[1]}_{0,4} a^{[1]}_{4,0} + \theta^{[1]}_{1,4} a^{[1]}_{4,1} + \theta^{[1]}_{2,4} a^{[1]}_{4,2} + \theta^{[1]}_{3,4} a^{[1]}_{4,3} & & \theta^{[1]}_{0,5} a^{[1]}_{4,0} + \theta^{[1]}_{1,5} a^{[1]}_{4,1} + \theta^{[1]}_{2,5} a^{[1]}_{4,2} + \theta^{[1]}_{3,5} a^{[1]}_{4,3} \\ \theta^{[1]}_{0,1} a^{[1]}_{5,0} + \theta^{[1]}_{1,1} a^{[1]}_{5,1} + \theta^{[1]}_{2,1} a^{[1]}_{5,2} + \theta^{[1]}_{3,1} a^{[1]}_{5,3} & & \theta^{[1]}_{0,2} a^{[1]}_{5,0} + \theta^{[1]}_{1,2} a^{[1]}_{5,1} + \theta^{[1]}_{2,2} a^{[1]}_{5,2} + \theta^{[1]}_{3,2} a^{[1]}_{5,3} & & \theta^{[1]}_{0,3} a^{[1]}_{5,0} + \theta^{[1]}_{1,3} a^{[1]}_{5,1} + \theta^{[1]}_{2,3} a^{[1]}_{5,2} + \theta^{[1]}_{3,3} a^{[1]}_{5,3} & & \theta^{[1]}_{0,4} a^{[1]}_{5,0} + \theta^{[1]}_{1,4} a^{[1]}_{5,1} + \theta^{[1]}_{2,4} a^{[1]}_{5,2} + \theta^{[1]}_{3,4} a^{[1]}_{5,3} & & \theta^{[1]}_{0,5} a^{[1]}_{5,0} + \theta^{[1]}_{1,5} a^{[1]}_{5,1} + \theta^{[1]}_{2,5} a^{[1]}_{5,2} + \theta^{[1]}_{3,5} a^{[1]}_{5,3} \\ \theta^{[1]}_{0,1} a^{[1]}_{6,0} + \theta^{[1]}_{1,1} a^{[1]}_{6,1} + \theta^{[1]}_{2,1} a^{[1]}_{6,2} + \theta^{[1]}_{3,1} a^{[1]}_{6,3} & & \theta^{[1]}_{0,2} a^{[1]}_{6,0} + \theta^{[1]}_{1,2} a^{[1]}_{6,1} + \theta^{[1]}_{2,2} a^{[1]}_{6,2} + \theta^{[1]}_{3,2} a^{[1]}_{6,3} & & \theta^{[1]}_{0,3} a^{[1]}_{6,0} + \theta^{[1]}_{1,3} a^{[1]}_{6,1} + \theta^{[1]}_{2,3} a^{[1]}_{6,2} + \theta^{[1]}_{3,3} a^{[1]}_{6,3} & & \theta^{[1]}_{0,4} a^{[1]}_{6,0} + \theta^{[1]}_{1,4} a^{[1]}_{6,1} + \theta^{[1]}_{2,4} a^{[1]}_{6,2} + \theta^{[1]}_{3,4} a^{[1]}_{6,3} & & \theta^{[1]}_{0,5} a^{[1]}_{6,0} + \theta^{[1]}_{1,5} a^{[1]}_{6,1} + \theta^{[1]}_{2,5} a^{[1]}_{6,2} + \theta^{[1]}_{3,5} a^{[1]}_{6,3} \\ \theta^{[1]}_{0,1} a^{[1]}_{7,0} + \theta^{[1]}_{1,1} a^{[1]}_{7,1} + \theta^{[1]}_{2,1} a^{[1]}_{7,2} + \theta^{[1]}_{3,1} a^{[1]}_{7,3} & & \theta^{[1]}_{0,2} a^{[1]}_{7,0} + \theta^{[1]}_{1,2} a^{[1]}_{7,1} + \theta^{[1]}_{2,2} a^{[1]}_{7,2} + \theta^{[1]}_{3,2} a^{[1]}_{7,3} & & \theta^{[1]}_{0,3} a^{[1]}_{7,0} + \theta^{[1]}_{1,3} a^{[1]}_{7,1} + \theta^{[1]}_{2,3} a^{[1]}_{7,2} + \theta^{[1]}_{3,3} a^{[1]}_{7,3} & & \theta^{[1]}_{0,4} a^{[1]}_{7,0} + \theta^{[1]}_{1,4} a^{[1]}_{7,1} + \theta^{[1]}_{2,4} a^{[1]}_{7,2} + \theta^{[1]}_{3,4} a^{[1]}_{7,3} & & \theta^{[1]}_{0,5} a^{[1]}_{7,0} + \theta^{[1]}_{1,5} a^{[1]}_{7,1} + \theta^{[1]}_{2,5} a^{[1]}_{7,2} + \theta^{[1]}_{3,5} a^{[1]}_{7,3} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{Z^{[2]}}\right\vert = \left \{ m \times u^{[2]} \right \} \]
\[ \]
\[ Z^{[2]} = \left( \begin{array}{Z2short} z^{[2]}_{1,1} & z^{[2]}_{1,2} & z^{[2]}_{1,3} & z^{[2]}_{1,4} & z^{[2]}_{1,5} \\ z^{[2]}_{2,1} & z^{[2]}_{2,2} & z^{[2]}_{2,3} & z^{[2]}_{2,4} & z^{[2]}_{2,5} \\ z^{[2]}_{3,1} & z^{[2]}_{3,2} & z^{[2]}_{3,3} & z^{[2]}_{3,4} & z^{[2]}_{3,5} \\ z^{[2]}_{4,1} & z^{[2]}_{4,2} & z^{[2]}_{4,3} & z^{[2]}_{4,4} & z^{[2]}_{4,5} \\ z^{[2]}_{5,1} & z^{[2]}_{5,2} & z^{[2]}_{5,3} & z^{[2]}_{5,4} & z^{[2]}_{5,5} \\ z^{[2]}_{6,1} & z^{[2]}_{6,2} & z^{[2]}_{6,3} & z^{[2]}_{6,4} & z^{[2]}_{6,5} \\ z^{[2]}_{7,1} & z^{[2]}_{7,2} & z^{[2]}_{7,3} & z^{[2]}_{7,4} & z^{[2]}_{7,5} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{Z^{[2]}}\right\vert = \left \{ m \times u^{[2]} \right \} \]
\[ \]
In R the dot product operator is “%*%”.
\[ \]
Z2 <- (A1 %*% Theta1)
show(Z2)
## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.4617647 1.208542 1.078323 0.9779862 1.0335097
## [2,] 0.5214699 1.292435 1.163272 1.0253858 1.0936839
## [3,] 1.5820906 1.254571 1.137868 2.3669577 0.7194696
## [4,] 0.5214699 1.292435 1.163272 1.0253858 1.0936839
## [5,] 1.6675871 1.301988 1.178516 2.4604799 0.7297545
## [6,] 1.7475491 1.302124 1.218897 2.5514071 0.7398720
## [7,] 1.8429077 1.391454 1.291925 2.6458972 0.7777147
\[ \]
\[ \]
The Activation Function (also called the "squashing function"), \( g(Z^{[l]}) \), in this case is the Sigmoid function. Other potential Activation Functions include the hyperbolic tangent function, softmax, and the unit step function.
\[ \]
\[ H^{[2]} = g(Z^{[2]}) = \left( \begin{array}{H2} \frac{1}{1+\exp(-z^{[2]}_{1,1})} & & \frac{1}{1+\exp(-z^{[2]}_{1,2})} & & \frac{1}{1+\exp(-z^{[2]}_{7,3})} & & \frac{1}{1+\exp(-z^{[2]}_{1,4})} & & \frac{1}{1+\exp(-z^{[2]}_{1,5})} \\ \frac{1}{1+\exp(-z^{[2]}_{2,1})} & & \frac{1}{1+\exp(-z^{[2]}_{2,2})} & & \frac{1}{1+\exp(-z^{[2]}_{7,3})} & & \frac{1}{1+\exp(-z^{[2]}_{2,4})} & & \frac{1}{1+\exp(-z^{[2]}_{2,5})} \\ \frac{1}{1+\exp(-z^{[2]}_{3,1})} & & \frac{1}{1+\exp(-z^{[2]}_{3,2})} & & \frac{1}{1+\exp(-z^{[2]}_{7,3})} & & \frac{1}{1+\exp(-z^{[2]}_{3,4})} & & \frac{1}{1+\exp(-z^{[2]}_{3,5})} \\ \frac{1}{1+\exp(-z^{[2]}_{4,1})} & & \frac{1}{1+\exp(-z^{[2]}_{4,2})} & & \frac{1}{1+\exp(-z^{[2]}_{7,3})} & & \frac{1}{1+\exp(-z^{[2]}_{4,4})} & & \frac{1}{1+\exp(-z^{[2]}_{4,5})} \\ \frac{1}{1+\exp(-z^{[2]}_{5,1})} & & \frac{1}{1+\exp(-z^{[2]}_{5,2})} & & \frac{1}{1+\exp(-z^{[2]}_{7,3})} & & \frac{1}{1+\exp(-z^{[2]}_{5,4})} & & \frac{1}{1+\exp(-z^{[2]}_{5,5})} \\ \frac{1}{1+\exp(-z^{[2]}_{6,1})} & & \frac{1}{1+\exp(-z^{[2]}_{6,2})} & & \frac{1}{1+\exp(-z^{[2]}_{7,3})} & & \frac{1}{1+\exp(-z^{[2]}_{6,4})} & & \frac{1}{1+\exp(-z^{[2]}_{6,5})} \\ \frac{1}{1+\exp(-z^{[2]}_{7,1})} & & \frac{1}{1+\exp(-z^{[2]}_{7,2})} & & \frac{1}{1+\exp(-z^{[2]}_{7,3})} & & \frac{1}{1+\exp(-z^{[2]}_{7,4})} & & \frac{1}{1+\exp(-z^{[2]}_{7,5})} \\ \end{array} \right ) = \left( \begin{array}{} h^{[2]}_{1,1} & h^{[2]}_{1,2} & h^{[2]}_{1,3} & h^{[2]}_{1,4} & h^{[2]}_{1,5}\\ h^{[2]}_{2,1} & h^{[2]}_{2,2} & h^{[2]}_{2,3} & h^{[2]}_{2,4} & h^{[2]}_{2,5}\\ h^{[2]}_{3,1} & h^{[2]}_{3,2} & h^{[2]}_{3,3} & h^{[2]}_{3,4} & h^{[2]}_{3,5}\\ h^{[2]}_{4,1} & h^{[2]}_{4,2} & h^{[2]}_{4,3} & h^{[2]}_{4,4} & h^{[2]}_{4,5}\\ h^{[2]}_{5,1} & h^{[2]}_{5,2} & h^{[2]}_{5,3} & h^{[2]}_{5,4} & h^{[2]}_{5,5}\\ h^{[2]}_{6,1} & h^{[2]}_{6,2} & h^{[2]}_{6,3} & h^{[2]}_{6,4} & h^{[2]}_{6,5}\\ h^{[2]}_{7,1} & h^{[2]}_{7,2} & h^{[2]}_{7,3} & h^{[2]}_{7,4} & h^{[2]}_{7,5}\\ \end{array} \right ) \]
\[ \]
\[ \color{gray} \left\vert{H^{[2]}}\right\vert = \left \{ m \times u^{[2]} \right \} \]
\[ \]
\[ \]
\( H^{[2]} \) now becomes our input, \( A^{[2]} \), for the third layer (i.e. the second hidden layer).
\[ \]
Again, to accommodate a bias term we append a column of ones to our (new) input matrix.
\[ \]
\[ A^{[2]} = \left( \begin{array}{A2prior} 1 & h^{[2]}_{1,1} & h^{[2]}_{1,2} & h^{[2]}_{1,3} & h^{[2]}_{1,4} & h^{[2]}_{1,5}\\ 1 & h^{[2]}_{2,1} & h^{[2]}_{2,2} & h^{[2]}_{2,3} & h^{[2]}_{2,4} & h^{[2]}_{2,5}\\ 1 & h^{[2]}_{3,1} & h^{[2]}_{3,2} & h^{[2]}_{3,3} & h^{[2]}_{3,4} & h^{[2]}_{3,5}\\ 1 & h^{[2]}_{4,1} & h^{[2]}_{4,2} & h^{[2]}_{4,3} & h^{[2]}_{4,4} & h^{[2]}_{4,5}\\ 1 & h^{[2]}_{5,1} & h^{[2]}_{5,2} & h^{[2]}_{5,3} & h^{[2]}_{5,4} & h^{[2]}_{5,5}\\ 1 & h^{[2]}_{6,1} & h^{[2]}_{6,2} & h^{[2]}_{6,3} & h^{[2]}_{6,4} & h^{[2]}_{6,5}\\ 1 & h^{[2]}_{7,1} & h^{[2]}_{7,2} & h^{[2]}_{7,3} & h^{[2]}_{7,4} & h^{[2]}_{7,5}\\ \end{array} \right) = \left( \begin{array}{A2} a^{[2]}_{1,0} & a^{[2]}_{1,1} & a^{[2]}_{1,2} & a^{[2]}_{1,3} & a^{[2]}_{1,4} & a^{[2]}_{1,5} \\ a^{[2]}_{2,0} & a^{[2]}_{2,1} & a^{[2]}_{2,2} & a^{[2]}_{2,3} & a^{[2]}_{2,4} & a^{[2]}_{2,5} \\ a^{[2]}_{3,0} & a^{[2]}_{3,1} & a^{[2]}_{3,2} & a^{[2]}_{3,3} & a^{[2]}_{3,4} & a^{[2]}_{3,5} \\ a^{[2]}_{4,0} & a^{[2]}_{4,1} & a^{[2]}_{4,2} & a^{[2]}_{4,3} & a^{[2]}_{4,4} & a^{[2]}_{4,5} \\ a^{[2]}_{5,0} & a^{[2]}_{5,1} & a^{[2]}_{5,2} & a^{[2]}_{5,3} & a^{[2]}_{5,4} & a^{[2]}_{5,5} \\ a^{[2]}_{6,0} & a^{[2]}_{6,1} & a^{[2]}_{6,2} & a^{[2]}_{6,3} & a^{[2]}_{6,4} & a^{[2]}_{6,5} \\ a^{[2]}_{7,0} & a^{[2]}_{7,1} & a^{[2]}_{7,2} & a^{[2]}_{7,3} & a^{[2]}_{7,4} & a^{[2]}_{7,5} \\ \end{array} \right ) \]
\[ \]
\[ \color{gray} \left\vert{A^{[2]}}\right\vert = \left \{ m \times (u^{[2]} + 1) \right \} \]
\[ \]
A2 <- 1/(1 + exp(-Z2))
A2 <- cbind(rep(1, 7), A2)
show(A2)
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1 0.6134327 0.7700410 0.7461764 0.7267085 0.7375958
## [2,] 1 0.6274914 0.7845591 0.7619267 0.7360204 0.7490748
## [3,] 1 0.8295004 0.7780901 0.7572880 0.9142727 0.6724902
## [4,] 1 0.6274914 0.7845591 0.7619267 0.7360204 0.7490748
## [5,] 1 0.8412539 0.7861694 0.7646810 0.9213245 0.6747514
## [6,] 1 0.8516434 0.7861922 0.7718694 0.9276680 0.6769679
## [7,] 1 0.8632922 0.8008242 0.7844729 0.9337577 0.6851874
\[ \]
\[ \Theta^{[2]} = \left( \begin{array}{Theta2} \theta^{[2]}_{0,1} & \theta^{[2]}_{0,2} & \theta^{[2]}_{0,3} & \theta^{[2]}_{0,4} & \theta^{[2]}_{0,5} & \theta^{[2]}_{0,6} \\ \theta^{[2]}_{1,1} & \theta^{[2]}_{1,2} & \theta^{[2]}_{1,3} & \theta^{[2]}_{1,4} & \theta^{[2]}_{1,5} & \theta^{[2]}_{1,6} \\ \theta^{[2]}_{2,1} & \theta^{[2]}_{2,2} & \theta^{[2]}_{2,3} & \theta^{[2]}_{2,4} & \theta^{[2]}_{2,5} & \theta^{[2]}_{2,6} \\ \theta^{[2]}_{3,1} & \theta^{[2]}_{3,2} & \theta^{[2]}_{3,3} & \theta^{[2]}_{3,4} & \theta^{[2]}_{3,5} & \theta^{[2]}_{3,6} \\ \theta^{[2]}_{4,1} & \theta^{[2]}_{4,2} & \theta^{[2]}_{4,3} & \theta^{[2]}_{4,4} & \theta^{[2]}_{4,5} & \theta^{[2]}_{4,6} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{\Theta^{[2]}}\right\vert = \left \{ (u^{[2]} + 1 ) \times u^{[3]} \right \} \]
\[ \]
Theta2 <- matrix(runif(24), ncol = 4) ## (u[2]+1)*u[3] = 6 * 4 = 24
show(Theta2)
## [,1] [,2] [,3] [,4]
## [1,] 0.8892086 0.3494487 0.3163603 0.683983234
## [2,] 0.2962099 0.9918466 0.7734901 0.003920189
## [3,] 0.7344368 0.9821542 0.7242544 0.091255618
## [4,] 0.2114049 0.1363947 0.2570233 0.813585034
## [5,] 0.1020030 0.2169977 0.1734081 0.164268804
## [6,] 0.3134118 0.7093792 0.2547354 0.578385592
\[ \]
\[ Z^{[3]} = A^{[2]} \cdot \Theta^{[2]} = \left( \begin{array}{A1} a^{[2]}_{1,0} & a^{[2]}_{1,1} & a^{[2]}_{1,2} & a^{[2]}_{1,3} \\ a^{[2]}_{2,0} & a^{[2]}_{2,1} & a^{[2]}_{2,2} & a^{[2]}_{2,3} \\ a^{[2]}_{3,0} & a^{[2]}_{3,1} & a^{[2]}_{3,2} & a^{[2]}_{3,3} \\ a^{[2]}_{4,0} & a^{[2]}_{4,1} & a^{[2]}_{4,2} & a^{[2]}_{4,3} \\ a^{[2]}_{5,0} & a^{[2]}_{5,1} & a^{[2]}_{5,2} & a^{[2]}_{5,3} \\ a^{[2]}_{6,0} & a^{[2]}_{6,1} & a^{[2]}_{6,2} & a^{[2]}_{6,3} \\ a^{[2]}_{7,0} & a^{[2]}_{7,1} & a^{[2]}_{7,2} & a^{[2]}_{7,3} \\ \end{array} \right ) \cdot \left( \begin{array}{Theta1} \theta^{[2]}_{0,1} & \theta^{[2]}_{0,2} & \theta^{[2]}_{0,3} & \theta^{[2]}_{0,4} & \theta^{[2]}_{0,5} \\ \theta^{[2]}_{1,1} & \theta^{[2]}_{1,2} & \theta^{[2]}_{1,3} & \theta^{[2]}_{1,4} & \theta^{[2]}_{1,5} \\ \theta^{[2]}_{2,1} & \theta^{[2]}_{2,2} & \theta^{[2]}_{2,3} & \theta^{[2]}_{2,4} & \theta^{[2]}_{2,5} \\ \theta^{[2]}_{3,1} & \theta^{[2]}_{3,2} & \theta^{[2]}_{3,3} & \theta^{[2]}_{3,4} & \theta^{[2]}_{3,5} \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{Z^{[3]}}\right\vert = \left \{ m \times (u^{[2]}+1) \right \} \cdot \left \{ (u^{[2]} + 1 ) \times u^{[2]} \right \} \]
\[ \]\[ Z^{[3]} = \left( \begin{array}{Z2} \theta^{[2]}_{0,1} a^{[2]}_{1,0} + \theta^{[2]}_{1,1} a^{[2]}_{1,1} + \theta^{[2]}_{2,1} a^{[2]}_{1,2} + \theta^{[2]}_{3,1} a^{[2]}_{1,3} & & \theta^{[2]}_{0,2} a^{[2]}_{1,0} + \theta^{[2]}_{1,2} a^{[2]}_{1,1} + \theta^{[2]}_{2,2} a^{[2]}_{1,2} + \theta^{[2]}_{3,2} a^{[2]}_{1,3} & & \theta^{[2]}_{0,3} a^{[2]}_{1,0} + \theta^{[2]}_{1,3} a^{[2]}_{1,1} + \theta^{[2]}_{2,3} a^{[2]}_{1,2} + \theta^{[2]}_{3,3} a^{[2]}_{1,3} & & \theta^{[2]}_{0,4} a^{[2]}_{1,0} + \theta^{[2]}_{1,4} a^{[2]}_{1,1} + \theta^{[2]}_{2,4} a^{[2]}_{1,2} + \theta^{[2]}_{3,4} a^{[2]}_{1,3} & & \theta^{[2]}_{0,5} a^{[2]}_{1,0} + \theta^{[2]}_{1,5} a^{[2]}_{1,1} + \theta^{[2]}_{2,5} a^{[2]}_{1,2} + \theta^{[2]}_{3,5} a^{[2]}_{1,3} \\ \theta^{[2]}_{0,1} a^{[2]}_{2,0} + \theta^{[2]}_{1,1} a^{[2]}_{2,1} + \theta^{[2]}_{2,1} a^{[2]}_{2,2} + \theta^{[2]}_{3,1} a^{[2]}_{2,3} & & \theta^{[2]}_{0,2} a^{[2]}_{2,0} + \theta^{[2]}_{1,2} a^{[2]}_{2,1} + \theta^{[2]}_{2,2} a^{[2]}_{2,2} + \theta^{[2]}_{3,2} a^{[2]}_{2,3} & & \theta^{[2]}_{0,3} a^{[2]}_{2,0} + \theta^{[2]}_{1,3} a^{[2]}_{2,1} + \theta^{[2]}_{2,3} a^{[2]}_{2,2} + \theta^{[2]}_{3,3} a^{[2]}_{2,3} & & \theta^{[2]}_{0,4} a^{[2]}_{2,0} + \theta^{[2]}_{1,4} a^{[2]}_{2,1} + \theta^{[2]}_{2,4} a^{[2]}_{2,2} + \theta^{[2]}_{3,4} a^{[2]}_{2,3} & & \theta^{[2]}_{0,5} a^{[2]}_{2,0} + \theta^{[2]}_{1,5} a^{[2]}_{2,1} + \theta^{[2]}_{2,5} a^{[2]}_{2,2} + \theta^{[2]}_{3,5} a^{[2]}_{2,3} \\ \theta^{[2]}_{0,1} a^{[2]}_{3,0} + \theta^{[2]}_{1,1} a^{[2]}_{3,1} + \theta^{[2]}_{2,1} a^{[2]}_{3,2} + \theta^{[2]}_{3,1} a^{[2]}_{3,3} & & \theta^{[2]}_{0,2} a^{[2]}_{3,0} + \theta^{[2]}_{1,2} a^{[2]}_{3,1} + \theta^{[2]}_{2,2} a^{[2]}_{3,2} + \theta^{[2]}_{3,2} a^{[2]}_{3,3} & & \theta^{[2]}_{0,3} a^{[2]}_{3,0} + \theta^{[2]}_{1,3} a^{[2]}_{3,1} + \theta^{[2]}_{2,3} a^{[2]}_{3,2} + \theta^{[2]}_{3,3} a^{[2]}_{3,3} & & \theta^{[2]}_{0,4} a^{[2]}_{3,0} + \theta^{[2]}_{1,4} a^{[2]}_{3,1} + \theta^{[2]}_{2,4} a^{[2]}_{3,2} + \theta^{[2]}_{3,4} a^{[2]}_{3,3} & & \theta^{[2]}_{0,5} a^{[2]}_{3,0} + \theta^{[2]}_{1,5} a^{[2]}_{3,1} + \theta^{[2]}_{2,5} a^{[2]}_{3,2} + \theta^{[2]}_{3,5} a^{[2]}_{3,3} \\ \theta^{[2]}_{0,1} a^{[2]}_{4,0} + \theta^{[2]}_{1,1} a^{[2]}_{4,1} + \theta^{[2]}_{2,1} a^{[2]}_{4,2} + \theta^{[2]}_{3,1} a^{[2]}_{4,3} & & \theta^{[2]}_{0,2} a^{[2]}_{4,0} + \theta^{[2]}_{1,2} a^{[2]}_{4,1} + \theta^{[2]}_{2,2} a^{[2]}_{4,2} + \theta^{[2]}_{3,2} a^{[2]}_{4,3} & & \theta^{[2]}_{0,3} a^{[2]}_{4,0} + \theta^{[2]}_{1,3} a^{[2]}_{4,1} + \theta^{[2]}_{2,3} a^{[2]}_{4,2} + \theta^{[2]}_{3,3} a^{[2]}_{4,3} & & \theta^{[2]}_{0,4} a^{[2]}_{4,0} + \theta^{[2]}_{1,4} a^{[2]}_{4,1} + \theta^{[2]}_{2,4} a^{[2]}_{4,2} + \theta^{[2]}_{3,4} a^{[2]}_{4,3} & & \theta^{[2]}_{0,5} a^{[2]}_{4,0} + \theta^{[2]}_{1,5} a^{[2]}_{4,1} + \theta^{[2]}_{2,5} a^{[2]}_{4,2} + \theta^{[2]}_{3,5} a^{[2]}_{4,3} \\ \theta^{[2]}_{0,1} a^{[2]}_{5,0} + \theta^{[2]}_{1,1} a^{[2]}_{5,1} + \theta^{[2]}_{2,1} a^{[2]}_{5,2} + \theta^{[2]}_{3,1} a^{[2]}_{5,3} & & \theta^{[2]}_{0,2} a^{[2]}_{5,0} + \theta^{[2]}_{1,2} a^{[2]}_{5,1} + \theta^{[2]}_{2,2} a^{[2]}_{5,2} + \theta^{[2]}_{3,2} a^{[2]}_{5,3} & & \theta^{[2]}_{0,3} a^{[2]}_{5,0} + \theta^{[2]}_{1,3} a^{[2]}_{5,1} + \theta^{[2]}_{2,3} a^{[2]}_{5,2} + \theta^{[2]}_{3,3} a^{[2]}_{5,3} & & \theta^{[2]}_{0,4} a^{[2]}_{5,0} + \theta^{[2]}_{1,4} a^{[2]}_{5,1} + \theta^{[2]}_{2,4} a^{[2]}_{5,2} + \theta^{[2]}_{3,4} a^{[2]}_{5,3} & & \theta^{[2]}_{0,5} a^{[2]}_{5,0} + \theta^{[2]}_{1,5} a^{[2]}_{5,1} + \theta^{[2]}_{2,5} a^{[2]}_{5,2} + \theta^{[2]}_{3,5} a^{[2]}_{5,3} \\ \theta^{[2]}_{0,1} a^{[2]}_{6,0} + \theta^{[2]}_{1,1} a^{[2]}_{6,1} + \theta^{[2]}_{2,1} a^{[2]}_{6,2} + \theta^{[2]}_{3,1} a^{[2]}_{6,3} & & \theta^{[2]}_{0,2} a^{[2]}_{6,0} + \theta^{[2]}_{1,2} a^{[2]}_{6,1} + \theta^{[2]}_{2,2} a^{[2]}_{6,2} + \theta^{[2]}_{3,2} a^{[2]}_{6,3} & & \theta^{[2]}_{0,3} a^{[2]}_{6,0} + \theta^{[2]}_{1,3} a^{[2]}_{6,1} + \theta^{[2]}_{2,3} a^{[2]}_{6,2} + \theta^{[2]}_{3,3} a^{[2]}_{6,3} & & \theta^{[2]}_{0,4} a^{[2]}_{6,0} + \theta^{[2]}_{1,4} a^{[2]}_{6,1} + \theta^{[2]}_{2,4} a^{[2]}_{6,2} + \theta^{[2]}_{3,4} a^{[2]}_{6,3} & & \theta^{[2]}_{0,5} a^{[2]}_{6,0} + \theta^{[2]}_{1,5} a^{[2]}_{6,1} + \theta^{[2]}_{2,5} a^{[2]}_{6,2} + \theta^{[2]}_{3,5} a^{[2]}_{6,3} \\ \theta^{[2]}_{0,1} a^{[2]}_{7,0} + \theta^{[2]}_{1,1} a^{[2]}_{7,1} + \theta^{[2]}_{2,1} a^{[2]}_{7,2} + \theta^{[2]}_{3,1} a^{[2]}_{7,3} & & \theta^{[2]}_{0,2} a^{[2]}_{7,0} + \theta^{[2]}_{1,2} a^{[2]}_{7,1} + \theta^{[2]}_{2,2} a^{[2]}_{7,2} + \theta^{[2]}_{3,2} a^{[2]}_{7,3} & & \theta^{[2]}_{0,3} a^{[2]}_{7,0} + \theta^{[2]}_{1,3} a^{[2]}_{7,1} + \theta^{[2]}_{2,3} a^{[2]}_{7,2} + \theta^{[2]}_{3,3} a^{[2]}_{7,3} & & \theta^{[2]}_{0,4} a^{[2]}_{7,0} + \theta^{[2]}_{1,4} a^{[2]}_{7,1} + \theta^{[2]}_{2,4} a^{[2]}_{7,2} + \theta^{[2]}_{3,4} a^{[2]}_{7,3} & & \theta^{[2]}_{0,5} a^{[2]}_{7,0} + \theta^{[2]}_{1,5} a^{[2]}_{7,1} + \theta^{[2]}_{2,5} a^{[2]}_{7,2} + \theta^{[2]}_{3,5} a^{[2]}_{7,3} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{Z^{[3]}}\right\vert = \left \{ m \times u^{[2]} \right \} \]
\[ \]
\[ Z^{[3]} = \left( \begin{array}{Z2short} z^{[3]}_{1,1} & z^{[3]}_{1,2} & z^{[3]}_{1,3} & z^{[3]}_{1,4} \\ z^{[3]}_{2,1} & z^{[3]}_{2,2} & z^{[3]}_{2,3} & z^{[3]}_{2,4} \\ z^{[3]}_{3,1} & z^{[3]}_{3,2} & z^{[3]}_{3,3} & z^{[3]}_{3,4} \\ z^{[3]}_{4,1} & z^{[3]}_{4,2} & z^{[3]}_{4,3} & z^{[3]}_{4,4} \\ z^{[3]}_{5,1} & z^{[3]}_{5,2} & z^{[3]}_{5,3} & z^{[3]}_{5,4} \\ z^{[3]}_{6,1} & z^{[3]}_{6,2} & z^{[3]}_{6,3} & z^{[3]}_{6,4} \\ z^{[3]}_{7,1} & z^{[3]}_{7,2} & z^{[3]}_{7,3} & z^{[3]}_{7,4} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{Z^{[3]}}\right\vert = \left \{ m \times u^{[2]} \right \} \]
\[ \]
Z3 <- (A2 %*% Theta2)
show(Z3)
## [,1] [,2] [,3] [,4]
## [1,] 2.099503 2.496883 1.854244 1.909727
## [2,] 2.122207 2.537398 1.884220 1.932090
## [3,] 2.170492 2.715126 2.045996 1.913503
## [4,] 2.122207 2.537398 1.884220 1.932090
## [5,] 2.182898 2.738861 2.064637 1.922768
## [6,] 2.188854 2.753118 2.076202 1.930983
## [7,] 2.208912 2.787914 2.102199 1.948372
\[ \]
\[ \]
The Activation Function in this case is the Sigmoid function.
\[ \]
\[ H^{[3]} = g(Z^{[3]}) = \left( \begin{array}{H2} \frac{1}{1+\exp(-z^{[3]}_{1,1})} & & \frac{1}{1+\exp(-z^{[3]}_{1,2})} & & \frac{1}{1+\exp(-z^{[3]}_{7,3})} & & \frac{1}{1+\exp(-z^{[3]}_{7,4})} \\ \frac{1}{1+\exp(-z^{[3]}_{2,1})} & & \frac{1}{1+\exp(-z^{[3]}_{2,2})} & & \frac{1}{1+\exp(-z^{[3]}_{7,3})} & & \frac{1}{1+\exp(-z^{[3]}_{7,4})} \\ \frac{1}{1+\exp(-z^{[3]}_{3,1})} & & \frac{1}{1+\exp(-z^{[3]}_{3,2})} & & \frac{1}{1+\exp(-z^{[3]}_{7,3})} & & \frac{1}{1+\exp(-z^{[3]}_{7,4})} \\ \frac{1}{1+\exp(-z^{[3]}_{4,1})} & & \frac{1}{1+\exp(-z^{[3]}_{4,2})} & & \frac{1}{1+\exp(-z^{[3]}_{7,3})} & & \frac{1}{1+\exp(-z^{[3]}_{7,4})} \\ \frac{1}{1+\exp(-z^{[3]}_{5,1})} & & \frac{1}{1+\exp(-z^{[3]}_{5,2})} & & \frac{1}{1+\exp(-z^{[3]}_{7,3})} & & \frac{1}{1+\exp(-z^{[3]}_{7,4})} \\ \frac{1}{1+\exp(-z^{[3]}_{6,1})} & & \frac{1}{1+\exp(-z^{[3]}_{6,2})} & & \frac{1}{1+\exp(-z^{[3]}_{7,3})} & & \frac{1}{1+\exp(-z^{[3]}_{7,4})} \\ \frac{1}{1+\exp(-z^{[3]}_{7,1})} & & \frac{1}{1+\exp(-z^{[3]}_{7,2})} & & \frac{1}{1+\exp(-z^{[3]}_{7,3})} & & \frac{1}{1+\exp(-z^{[3]}_{7,4})} \\ \end{array} \right ) = \left( \begin{array}{} h^{[3]}_{1,1} & h^{[3]}_{1,2} & h^{[3]}_{1,3} & h^{[3]}_{1,4}\\ h^{[3]}_{2,1} & h^{[3]}_{2,2} & h^{[3]}_{2,3} & h^{[3]}_{2,4}\\ h^{[3]}_{3,1} & h^{[3]}_{3,2} & h^{[3]}_{3,3} & h^{[3]}_{3,4}\\ h^{[3]}_{4,1} & h^{[3]}_{4,2} & h^{[3]}_{4,3} & h^{[3]}_{4,4}\\ h^{[3]}_{5,1} & h^{[3]}_{5,2} & h^{[3]}_{5,3} & h^{[3]}_{5,4}\\ h^{[3]}_{6,1} & h^{[3]}_{6,2} & h^{[3]}_{6,3} & h^{[3]}_{6,4}\\ h^{[3]}_{7,1} & h^{[3]}_{7,2} & h^{[3]}_{7,3} & h^{[3]}_{7,4}\\ \end{array} \right ) \]
\[ \]
\[ \color{gray} \left\vert{H^{[3]}}\right\vert = \left \{ m \times u^{[3]} \right \} \]
\[ \]
\[ A^{[2]} = \left( \begin{array}{A2prior} 1 & h^{[2]}_{1,1} & h^{[2]}_{1,2} & h^{[2]}_{1,3} & h^{[2]}_{1,4}\\ 1 & h^{[2]}_{2,1} & h^{[2]}_{2,2} & h^{[2]}_{2,3} & h^{[2]}_{2,4}\\ 1 & h^{[2]}_{3,1} & h^{[2]}_{3,2} & h^{[2]}_{3,3} & h^{[2]}_{3,4}\\ 1 & h^{[2]}_{4,1} & h^{[2]}_{4,2} & h^{[2]}_{4,3} & h^{[2]}_{4,4}\\ 1 & h^{[2]}_{5,1} & h^{[2]}_{5,2} & h^{[2]}_{5,3} & h^{[2]}_{5,4}\\ 1 & h^{[2]}_{6,1} & h^{[2]}_{6,2} & h^{[2]}_{6,3} & h^{[2]}_{6,4}\\ 1 & h^{[2]}_{7,1} & h^{[2]}_{7,2} & h^{[2]}_{7,3} & h^{[2]}_{7,4}\\ \end{array} \right) = \left( \begin{array}{A2} a^{[2]}_{1,0} & a^{[2]}_{1,1} & a^{[2]}_{1,2} & a^{[2]}_{1,3} & a^{[2]}_{1,4} \\ a^{[2]}_{2,0} & a^{[2]}_{2,1} & a^{[2]}_{2,2} & a^{[2]}_{2,3} & a^{[2]}_{2,4} \\ a^{[2]}_{3,0} & a^{[2]}_{3,1} & a^{[2]}_{3,2} & a^{[2]}_{3,3} & a^{[2]}_{3,4} \\ a^{[2]}_{4,0} & a^{[2]}_{4,1} & a^{[2]}_{4,2} & a^{[2]}_{4,3} & a^{[2]}_{4,4} \\ a^{[2]}_{5,0} & a^{[2]}_{5,1} & a^{[2]}_{5,2} & a^{[2]}_{5,3} & a^{[2]}_{5,4} \\ a^{[2]}_{6,0} & a^{[2]}_{6,1} & a^{[2]}_{6,2} & a^{[2]}_{6,3} & a^{[2]}_{6,4} \\ a^{[2]}_{7,0} & a^{[2]}_{7,1} & a^{[2]}_{7,2} & a^{[2]}_{7,3} & a^{[2]}_{7,4} \\ \end{array} \right ) \]
\[ \]
\[ \color{gray} \left\vert{A^{[2]}}\right\vert = \left \{ m \times (u^{[2]} + 1) \right \} \]
\[ \]
A2 <- 1/(1 + exp(-Z2))
A2 <- cbind(rep(1, 7), A2)
show(A2)
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 0.7704 0.7558 0.7704 0.7558
## [2,] 1 0.7881 0.7695 0.7704 0.7558
## [3,] 1 0.7737 0.8044 0.7704 0.7558
## [4,] 1 0.7881 0.7695 0.7704 0.7558
## [5,] 1 0.7814 0.8108 0.7704 0.7558
## [6,] 1 0.7907 0.8227 0.7704 0.7558
## [7,] 1 0.8040 0.8312 0.7704 0.7558
\[ \]
\[ \]
\[ \Theta^{[2]} = \left( \begin{array}{Theta2} \theta^{[2]}_{0,1} & \theta^{[2]}_{0,2} & \theta^{[2]}_{0,3} \\ \theta^{[2]}_{1,1} & \theta^{[2]}_{1,2} & \theta^{[2]}_{1,3} \\ \theta^{[2]}_{2,1} & \theta^{[2]}_{2,2} & \theta^{[2]}_{2,3} \\ \theta^{[2]}_{3,1} & \theta^{[2]}_{3,2} & \theta^{[2]}_{3,3} \\ \theta^{[2]}_{4,1} & \theta^{[2]}_{4,2} & \theta^{[2]}_{4,3} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{\Theta^{[2]}}\right\vert = \left \{ (u^{[2]} + 1 ) \times u^{[3]} \right \} \]
\[ \]
Theta2 <- matrix(runif(15), ncol = 3) ## (u[2]+1)*u[3] = 15
show(Theta2)
## [,1] [,2] [,3]
## [1,] 0.6249 0.9978 0.9978
## [2,] 0.1228 0.0649 0.9978
## [3,] 0.7716 0.7324 0.9978
## [4,] 0.7716 0.7324 0.9978
## [5,] 0.7716 0.7324 0.9978
\[ \]
\[ Z^{[3]} = A^{[2]} \cdot \Theta^{[2]} = \left( \begin{array}{A2} a^{[2]}_{1,0} & a^{[2]}_{1,1} & a^{[2]}_{1,2} & a^{[2]}_{1,3} & a^{[2]}_{1,4} \\ a^{[2]}_{2,0} & a^{[2]}_{2,1} & a^{[2]}_{2,2} & a^{[2]}_{2,3} & a^{[2]}_{2,4} \\ a^{[2]}_{3,0} & a^{[2]}_{3,1} & a^{[2]}_{3,2} & a^{[2]}_{3,3} & a^{[2]}_{3,4} \\ a^{[2]}_{4,0} & a^{[2]}_{4,1} & a^{[2]}_{4,2} & a^{[2]}_{4,3} & a^{[2]}_{4,4} \\ a^{[2]}_{5,0} & a^{[2]}_{5,1} & a^{[2]}_{5,2} & a^{[2]}_{5,3} & a^{[2]}_{5,4} \\ a^{[2]}_{6,0} & a^{[2]}_{6,1} & a^{[2]}_{6,2} & a^{[2]}_{6,3} & a^{[2]}_{6,4} \\ a^{[2]}_{7,0} & a^{[2]}_{7,1} & a^{[2]}_{7,2} & a^{[2]}_{7,3} & a^{[2]}_{7,4} \\ \end{array} \right ) \cdot \left( \begin{array}{Theta2} \theta^{[2]}_{0,1} & \theta^{[2]}_{0,2} & \theta^{[2]}_{0,3} \\ \theta^{[2]}_{1,1} & \theta^{[2]}_{1,2} & \theta^{[2]}_{1,3} \\ \theta^{[2]}_{2,1} & \theta^{[2]}_{2,2} & \theta^{[2]}_{2,3} \\ \theta^{[2]}_{3,1} & \theta^{[2]}_{3,2} & \theta^{[2]}_{3,3} \\ \theta^{[2]}_{4,1} & \theta^{[2]}_{4,2} & \theta^{[2]}_{4,3} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{Z^{[3]}}\right\vert = \{m \times (u^{[2]}+1) \} \cdot \{(u^{[2]}+1) \times u^{[3]} \} \]
\[ \]
\[ Z^{[3]} = \left( \begin{array}{Z3} \theta^{[2]}_{0,1} a^{[2]}_{1,0} + \theta^{[2]}_{1,1} a^{[2]}_{1,1} + \theta^{[2]}_{2,1} a^{[2]}_{1,2} + \theta^{[2]}_{3,1} a^{[2]}_{1,3} + \theta^{[2]}_{4,1} a^{[2]}_{1,4} & & \theta^{[2]}_{0,2} a^{[2]}_{1,0} + \theta^{[2]}_{1,2} a^{[2]}_{1,1} + \theta^{[2]}_{2,2} a^{[2]}_{1,2} + \theta^{[2]}_{3,2} a^{[2]}_{1,3} + \theta^{[2]}_{4,2} a^{[2]}_{1,4} & & \theta^{[2]}_{0,3} a^{[2]}_{1,0} + \theta^{[2]}_{1,3} a^{[2]}_{1,1} + \theta^{[2]}_{2,3} a^{[2]}_{1,2} + \theta^{[2]}_{3,3} a^{[2]}_{1,3} + \theta^{[2]}_{3,4} a^{[2]}_{1,4} \\ \theta^{[2]}_{0,1} a^{[2]}_{2,0} + \theta^{[2]}_{1,1} a^{[2]}_{2,1} + \theta^{[2]}_{2,1} a^{[2]}_{2,2} + \theta^{[2]}_{3,1} a^{[2]}_{2,3} + \theta^{[2]}_{4,1} a^{[2]}_{2,4} & & \theta^{[2]}_{0,2} a^{[2]}_{2,0} + \theta^{[2]}_{1,2} a^{[2]}_{2,1} + \theta^{[2]}_{2,2} a^{[2]}_{2,2} + \theta^{[2]}_{3,2} a^{[2]}_{2,3} + \theta^{[2]}_{4,2} a^{[2]}_{2,4} & & \theta^{[2]}_{0,3} a^{[2]}_{2,0} + \theta^{[2]}_{1,3} a^{[2]}_{2,1} + \theta^{[2]}_{2,3} a^{[2]}_{2,2} + \theta^{[2]}_{3,3} a^{[2]}_{2,3} + \theta^{[2]}_{4,3} a^{[2]}_{2,4} \\ \theta^{[2]}_{0,1} a^{[2]}_{3,0} + \theta^{[2]}_{1,1} a^{[2]}_{3,1} + \theta^{[2]}_{2,1} a^{[2]}_{3,2} + \theta^{[2]}_{3,1} a^{[2]}_{3,3} + \theta^{[2]}_{4,1} a^{[2]}_{3,4} & & \theta^{[2]}_{0,2} a^{[2]}_{3,0} + \theta^{[2]}_{1,2} a^{[2]}_{3,1} + \theta^{[2]}_{2,2} a^{[2]}_{3,2} + \theta^{[2]}_{3,2} a^{[2]}_{3,3} + \theta^{[2]}_{4,2} a^{[2]}_{3,4} & & \theta^{[2]}_{0,3} a^{[2]}_{3,0} + \theta^{[2]}_{1,3} a^{[2]}_{3,1} + \theta^{[2]}_{2,3} a^{[2]}_{3,2} + \theta^{[2]}_{3,3} a^{[2]}_{3,3} + \theta^{[2]}_{4,3} a^{[2]}_{3,4} \\ \theta^{[2]}_{0,1} a^{[2]}_{4,0} + \theta^{[2]}_{1,1} a^{[2]}_{4,1} + \theta^{[2]}_{2,1} a^{[2]}_{4,2} + \theta^{[2]}_{3,1} a^{[2]}_{4,3} + \theta^{[2]}_{4,1} a^{[2]}_{4,4} & & \theta^{[2]}_{0,2} a^{[2]}_{4,0} + \theta^{[2]}_{1,2} a^{[2]}_{4,1} + \theta^{[2]}_{2,2} a^{[2]}_{4,2} + \theta^{[2]}_{3,2} a^{[2]}_{4,3} + \theta^{[2]}_{4,2} a^{[2]}_{4,4} & & \theta^{[2]}_{0,3} a^{[2]}_{4,0} + \theta^{[2]}_{1,3} a^{[2]}_{4,1} + \theta^{[2]}_{2,3} a^{[2]}_{4,2} + \theta^{[2]}_{3,3} a^{[2]}_{4,3} + \theta^{[2]}_{4,3} a^{[2]}_{4,4} \\ \theta^{[2]}_{0,1} a^{[2]}_{5,0} + \theta^{[2]}_{1,1} a^{[2]}_{5,1} + \theta^{[2]}_{2,1} a^{[2]}_{5,2} + \theta^{[2]}_{3,1} a^{[2]}_{5,3} + \theta^{[2]}_{4,1} a^{[2]}_{5,4} & & \theta^{[2]}_{0,2} a^{[2]}_{5,0} + \theta^{[2]}_{1,2} a^{[2]}_{5,1} + \theta^{[2]}_{2,2} a^{[2]}_{5,2} + \theta^{[2]}_{3,2} a^{[2]}_{5,3} + \theta^{[2]}_{4,2} a^{[2]}_{5,4} & & \theta^{[2]}_{0,3} a^{[2]}_{5,0} + \theta^{[2]}_{1,3} a^{[2]}_{5,1} + \theta^{[2]}_{2,3} a^{[2]}_{5,2} + \theta^{[2]}_{3,3} a^{[2]}_{5,3} + \theta^{[2]}_{4,3} a^{[2]}_{5,4} \\ \theta^{[2]}_{0,1} a^{[2]}_{6,0} + \theta^{[2]}_{1,1} a^{[2]}_{6,1} + \theta^{[2]}_{2,1} a^{[2]}_{6,2} + \theta^{[2]}_{3,1} a^{[2]}_{6,3} + \theta^{[2]}_{4,1} a^{[2]}_{6,4} & & \theta^{[2]}_{0,2} a^{[2]}_{6,0} + \theta^{[2]}_{1,2} a^{[2]}_{6,1} + \theta^{[2]}_{2,2} a^{[2]}_{6,2} + \theta^{[2]}_{3,2} a^{[2]}_{6,3} + \theta^{[2]}_{4,2} a^{[2]}_{6,4} & & \theta^{[2]}_{0,3} a^{[2]}_{6,0} + \theta^{[2]}_{1,3} a^{[2]}_{6,1} + \theta^{[2]}_{2,3} a^{[2]}_{6,2} + \theta^{[2]}_{3,3} a^{[2]}_{6,3} + \theta^{[2]}_{4,3} a^{[2]}_{6,4} \\ \theta^{[2]}_{0,1} a^{[2]}_{7,0} + \theta^{[2]}_{1,1} a^{[2]}_{7,1} + \theta^{[2]}_{2,1} a^{[2]}_{7,2} + \theta^{[2]}_{3,1} a^{[2]}_{7,3} + \theta^{[2]}_{4,1} a^{[2]}_{7,4} & & \theta^{[2]}_{0,2} a^{[2]}_{7,0} + \theta^{[2]}_{1,2} a^{[2]}_{7,1} + \theta^{[2]}_{2,2} a^{[2]}_{7,2} + \theta^{[2]}_{3,2} a^{[2]}_{7,3} + \theta^{[2]}_{4,2} a^{[2]}_{7,4} & & \theta^{[2]}_{0,3} a^{[2]}_{7,0} + \theta^{[2]}_{1,3} a^{[2]}_{7,1} + \theta^{[2]}_{2,3} a^{[2]}_{7,2} + \theta^{[2]}_{3,3} a^{[2]}_{7,3} + \theta^{[2]}_{4,3} a^{[2]}_{7,4} \\ \end{array} \right) \]
\[ \]
\[ Z^{[3]} = \left( \begin{array}{Z2short} z^{[3]}_{1,1} & z^{[3]}_{1,2} & z^{[3]}_{1,3} \\ z^{[3]}_{2,1} & z^{[3]}_{2,2} & z^{[3]}_{2,3} \\ z^{[3]}_{3,1} & z^{[3]}_{3,2} & z^{[3]}_{3,3} \\ z^{[3]}_{4,1} & z^{[3]}_{4,2} & z^{[3]}_{4,3} \\ z^{[3]}_{5,1} & z^{[3]}_{5,2} & z^{[3]}_{5,3} \\ z^{[3]}_{6,1} & z^{[3]}_{6,2} & z^{[3]}_{6,3} \\ z^{[3]}_{7,1} & z^{[3]}_{7,2} & z^{[3]}_{7,3} \\ \end{array} \right) \]
\[ \]
\[ \color{gray} \left\vert{Z^{[3]}}\right\vert = \left \{ m \times u^{[3]} \right \} \]
\[ \]
Z3 <- (A2 %*% Theta2)
show(Z3)
## [,1] [,2] [,3]
## [1,] 1.303 1.601 1.601
## [2,] 1.315 1.612 1.601
## [3,] 1.341 1.637 1.601
## [4,] 1.315 1.612 1.601
## [5,] 1.346 1.642 1.601
## [6,] 1.357 1.652 1.601
## [7,] 1.365 1.659 1.601
\[ \]
The SoftMax function is often used as the Activation Function for the output layer in order to obtain action probabilities. Here, the Sigmoid function is used once more prior to applying the SoftMax function.
\[ \]
\[ A^{[3]} = \left( \begin{array}{A3} \frac{1}{1+\exp(-z^{[3]}_{1,1})} & & \frac{1}{1+\exp(-z^{[3]}_{1,2})} & & \frac{1}{1+\exp(-z^{[3]}_{1,3})} \\ \frac{1}{1+\exp(-z^{[3]}_{2,1})} & & \frac{1}{1+\exp(-z^{[3]}_{2,2})} & & \frac{1}{1+\exp(-z^{[3]}_{2,3})} \\ \frac{1}{1+\exp(-z^{[3]}_{3,1})} & & \frac{1}{1+\exp(-z^{[3]}_{3,2})} & & \frac{1}{1+\exp(-z^{[3]}_{3,3})} \\ \frac{1}{1+\exp(-z^{[3]}_{4,1})} & & \frac{1}{1+\exp(-z^{[3]}_{4,2})} & & \frac{1}{1+\exp(-z^{[3]}_{4,3})} \\ \frac{1}{1+\exp(-z^{[3]}_{5,1})} & & \frac{1}{1+\exp(-z^{[3]}_{5,2})} & & \frac{1}{1+\exp(-z^{[3]}_{5,3})} \\ \frac{1}{1+\exp(-z^{[3]}_{6,1})} & & \frac{1}{1+\exp(-z^{[3]}_{6,2})} & & \frac{1}{1+\exp(-z^{[3]}_{6,3})} \\ \frac{1}{1+\exp(-z^{[3]}_{7,1})} & & \frac{1}{1+\exp(-z^{[3]}_{7,2})} & & \frac{1}{1+\exp(-z^{[3]}_{7,3})} \\ \end{array} \right ) \]
\[ \]
\[ \color{gray} \left\vert{A^{[3]}}\right\vert = \left \{ m \times u^{[3]} \right \} \]
\[ \]
A3 <- 1/(1 + exp(-Z3))
show(A3)
## [,1] [,2] [,3]
## [1,] 0.7863 0.8322 0.8322
## [2,] 0.7884 0.8338 0.8322
## [3,] 0.7926 0.8371 0.8322
## [4,] 0.7884 0.8338 0.8322
## [5,] 0.7935 0.8379 0.8322
## [6,] 0.7952 0.8391 0.8322
## [7,] 0.7966 0.8401 0.8322
\[ \]
\[ \]
\[ J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m}\sum_{k=1}^{K}y_{i,k}log(h_{\theta}(x_{i})_{k}+(1-y_{i,k})log(1-(h_{\theta}(z_{i}))_{k})\right]+\frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{u^{[l]}}\sum_{r=1}^{u^{[l+1]}}(\theta^{[l]}_{r,i})^{2} \\ \frac{\partial }{\partial \theta^{[l]}_{r}} J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x_{i})-y_{i})) * x_{i,j} - \frac{\lambda}{m}\theta_{r}, \hspace{2em} \forall r \leq n \\ z_{i} = \theta_{0}+\theta_{1}x_{i,1}+...+\theta_{n}x_{i,n} = \theta_{0}+\sum_{r=1}^{n}\theta_{r}x_{i,r} \\ \]
\[ \]
\[ \delta^{[3]} = A^{[3]} - Y = \left( \begin{array}{A3} a^{[3]}_{1,1} & a^{[3]}_{1,2} & a^{[3]}_{1,3} \\ a^{[3]}_{2,1} & a^{[3]}_{2,2} & a^{[3]}_{2,3} \\ a^{[3]}_{3,1} & a^{[3]}_{3,2} & a^{[3]}_{3,3} \\ a^{[3]}_{4,1} & a^{[3]}_{4,2} & a^{[3]}_{4,3} \\ a^{[3]}_{5,1} & a^{[3]}_{5,2} & a^{[3]}_{5,3} \\ a^{[3]}_{6,1} & a^{[3]}_{6,2} & a^{[3]}_{6,3} \\ a^{[3]}_{7,1} & a^{[3]}_{7,2} & a^{[3]}_{7,3} \\ \end{array} \right ) - \left( \begin{array}{Y3} y_{1} & y_{1} & y_{1} \\ y_{2} & y_{2} & y_{2} \\ y_{3} & y_{3} & y_{3} \\ y_{4} & y_{4} & y_{4} \\ y_{5} & y_{5} & y_{5} \\ y_{6} & y_{6} & y_{6} \\ y_{7} & y_{7} & y_{7} \\ \end{array} \right ) = \left( \begin{array}{delta2} \delta^{[3]}_{1,1} & \delta^{[3]}_{1,2} & \delta^{[3]}_{1,3} \\ \delta^{[3]}_{2,1} & \delta^{[3]}_{2,2} & \delta^{[3]}_{2,3} \\ \delta^{[3]}_{3,1} & \delta^{[3]}_{3,2} & \delta^{[3]}_{3,3} \\ \delta^{[3]}_{4,1} & \delta^{[3]}_{4,2} & \delta^{[3]}_{4,3} \\ \delta^{[3]}_{5,1} & \delta^{[3]}_{5,2} & \delta^{[3]}_{5,3} \\ \delta^{[3]}_{6,1} & \delta^{[3]}_{6,2} & \delta^{[3]}_{6,3} \\ \delta^{[3]}_{7,1} & \delta^{[3]}_{7,2} & \delta^{[3]}_{7,3} \\ \end{array} \right) \\ \color{gray} \left\vert{\delta^{[3]}}\right\vert = \{ m \times u^{[3]} \} - \{ m \times 1 \} \cup \{ m \times 1 \} \cup \{ m \times 1 \} = \{ m \times u^{[3]} \} \]
\[ \]
\[ \delta^{[2]} = \left( \Theta^{[2]} \cdot (\delta^{[3]})^{T} \right)^{T} * A^{[2]} * (1-A^{[2]}) = \left( \left( \begin{array}{Theta2} \theta^{[2]}_{0,1} & \theta^{[2]}_{0,2} & \theta^{[2]}_{0,3} \\ \theta^{[2]}_{1,1} & \theta^{[2]}_{1,2} & \theta^{[2]}_{1,3} \\ \theta^{[2]}_{2,1} & \theta^{[2]}_{2,2} & \theta^{[2]}_{2,3} \\ \theta^{[2]}_{3,1} & \theta^{[2]}_{3,2} & \theta^{[2]}_{3,3} \\ \theta^{[2]}_{4,1} & \theta^{[2]}_{4,2} & \theta^{[2]}_{4,3} \\ \end{array} \right) \cdot \left( \begin{array}{delta2} \delta^{[3]}_{1,1} & \delta^{[3]}_{1,2} & \delta^{[3]}_{1,3} \\ \delta^{[3]}_{2,1} & \delta^{[3]}_{2,2} & \delta^{[3]}_{2,3} \\ \delta^{[3]}_{3,1} & \delta^{[3]}_{3,2} & \delta^{[3]}_{3,3} \\ \delta^{[3]}_{4,1} & \delta^{[3]}_{4,2} & \delta^{[3]}_{4,3} \\ \delta^{[3]}_{5,1} & \delta^{[3]}_{5,2} & \delta^{[3]}_{5,3} \\ \delta^{[3]}_{6,1} & \delta^{[3]}_{6,2} & \delta^{[3]}_{6,3} \\ \delta^{[3]}_{7,1} & \delta^{[3]}_{7,2} & \delta^{[3]}_{7,3} \\ \end{array} \right)^{T} \right)^{T} \times \left( \begin{array}{A2} a^{[2]}_{1,0} & a^{[2]}_{1,1} & a^{[2]}_{1,2} & a^{[2]}_{1,3} & a^{[2]}_{1,4} \\ a^{[2]}_{2,0} & a^{[2]}_{2,1} & a^{[2]}_{2,2} & a^{[2]}_{2,3} & a^{[2]}_{2,4} \\ a^{[2]}_{3,0} & a^{[2]}_{3,1} & a^{[2]}_{3,2} & a^{[2]}_{3,3} & a^{[2]}_{3,4} \\ a^{[2]}_{4,0} & a^{[2]}_{4,1} & a^{[2]}_{4,2} & a^{[2]}_{4,3} & a^{[2]}_{4,4} \\ a^{[2]}_{5,0} & a^{[2]}_{5,1} & a^{[2]}_{5,2} & a^{[2]}_{5,3} & a^{[2]}_{5,4} \\ a^{[2]}_{6,0} & a^{[2]}_{6,1} & a^{[2]}_{6,2} & a^{[2]}_{6,3} & a^{[2]}_{6,4} \\ a^{[2]}_{7,0} & a^{[2]}_{7,1} & a^{[2]}_{7,2} & a^{[2]}_{7,3} & a^{[2]}_{7,4} \\ \end{array} \right) \times \left( \begin{array}{A2} 1-a^{[2]}_{1,0} & 1-a^{[2]}_{1,1} & 1-a^{[2]}_{1,2} & 1-a^{[2]}_{1,3} & 1-a^{[2]}_{1,4} \\ 1-a^{[2]}_{2,0} & 1-a^{[2]}_{2,1} & 1-a^{[2]}_{2,2} & 1-a^{[2]}_{2,3} & 1-a^{[2]}_{2,4} \\ 1-a^{[2]}_{3,0} & 1-a^{[2]}_{3,1} & 1-a^{[2]}_{3,2} & 1-a^{[2]}_{3,3} & 1-a^{[2]}_{3,4} \\ 1-a^{[2]}_{4,0} & 1-a^{[2]}_{4,1} & 1-a^{[2]}_{4,2} & 1-a^{[2]}_{4,3} & 1-a^{[2]}_{4,4} \\ 1-a^{[2]}_{5,0} & 1-a^{[2]}_{5,1} & 1-a^{[2]}_{5,2} & 1-a^{[2]}_{5,3} & 1-a^{[2]}_{5,4} \\ 1-a^{[2]}_{6,0} & 1-a^{[2]}_{6,1} & 1-a^{[2]}_{6,2} & 1-a^{[2]}_{6,3} & 1-a^{[2]}_{6,4} \\ 1-a^{[2]}_{7,0} & 1-a^{[2]}_{7,1} & 1-a^{[2]}_{7,2} & 1-a^{[2]}_{7,3} & 1-a^{[2]}_{7,4} \\ \end{array} \right)\\ \\ \color{gray} \left\vert{\delta^{[2]}}\right\vert = \left( \left \{ (u^{[2]} + 1 ) \times u^{[3]} \right \} \cdot \left \{ m \times u^{[3]} \right \} ^{T} \right)^{T} * \left \{ m \times (u^{[2]} + 1) \right \} = \left \{ m \times (u^{[2]} + 1) \right \} \\ \]
\[ \]
\[ {\frac{\partial }{\partial \theta^{[l]}_{r}} J(\theta)}= \left( A^{[l]} \right)^{T} \cdot \delta^{[l+1]} \\ \]
\[ \]
\[ \frac{\partial }{\partial \theta^{[2]}_r} J(\theta) = ( A^{[2]} )^{T} \cdot \delta^{[3]} = \left( \begin{array}{A2} a^{[2]}_{1,0} & a^{[2]}_{1,1} & a^{[2]}_{1,2} & a^{[2]}_{1,3} & a^{[2]}_{1,4} \\ a^{[2]}_{2,0} & a^{[2]}_{2,1} & a^{[2]}_{2,2} & a^{[2]}_{2,3} & a^{[2]}_{2,4} \\ a^{[2]}_{3,0} & a^{[2]}_{3,1} & a^{[2]}_{3,2} & a^{[2]}_{3,3} & a^{[2]}_{3,4} \\ a^{[2]}_{4,0} & a^{[2]}_{4,1} & a^{[2]}_{4,2} & a^{[2]}_{4,3} & a^{[2]}_{4,4} \\ a^{[2]}_{5,0} & a^{[2]}_{5,1} & a^{[2]}_{5,2} & a^{[2]}_{5,3} & a^{[2]}_{5,4} \\ a^{[2]}_{6,0} & a^{[2]}_{6,1} & a^{[2]}_{6,2} & a^{[2]}_{6,3} & a^{[2]}_{6,4} \\ a^{[2]}_{7,0} & a^{[2]}_{7,1} & a^{[2]}_{7,2} & a^{[2]}_{7,3} & a^{[2]}_{7,4} \\ \end{array} \right) ^{T} \cdot \left( \begin{array}{delta2} \delta^{[3]}_{1,1} & \delta^{[3]}_{1,2} & \delta^{[3]}_{1,3} \\ \delta^{[3]}_{2,1} & \delta^{[3]}_{2,2} & \delta^{[3]}_{2,3} \\ \delta^{[3]}_{3,1} & \delta^{[3]}_{3,2} & \delta^{[3]}_{3,3} \\ \delta^{[3]}_{4,1} & \delta^{[3]}_{4,2} & \delta^{[3]}_{4,3} \\ \delta^{[3]}_{5,1} & \delta^{[3]}_{5,2} & \delta^{[3]}_{5,3} \\ \delta^{[3]}_{6,1} & \delta^{[3]}_{6,2} & \delta^{[3]}_{6,3} \\ \delta^{[3]}_{7,1} & \delta^{[3]}_{7,2} & \delta^{[3]}_{7,3} \\ \end{array} \right ) \\ \color{gray} \left\vert{\frac{\partial }{\partial \theta^{[2]}_{j}} J(\theta)}\right\vert = \left \{ m \times (u^{[2]} + 1) \right \}^{T} \cdot \{ m \times u^{[3]} \} = \left \{ (u^{[2]} + 1) \times u^{[3]} \right \} \]
\[ \]
\[ \frac{\partial }{\partial \theta^{[2]}_r} J(\theta) = \left( \begin{array}{J2} a^{[2]}_{1,0}\delta^{[3]}_{1,1} + a^{[2]}_{2,0}\delta^{[3]}_{2,1} + a^{[2]}_{3,0}\delta^{[3]}_{3,1} + a^{[2]}_{4,0}\delta^{[3]}_{4,1} + a^{[2]}_{5,0}\delta^{[3]}_{5,1}+ a^{[2]}_{6,0}\delta^{[3]}_{6,1}+ a^{[2]}_{7,0}\delta^{[3]}_{7,1} & & a^{[2]}_{1,0}\delta^{[3]}_{1,2} + a^{[2]}_{2,0}\delta^{[3]}_{2,2} + a^{[2]}_{3,0}\delta^{[3]}_{3,2} + a^{[2]}_{4,0}\delta^{[3]}_{4,2} + a^{[2]}_{5,0}\delta^{[3]}_{5,2}+ a^{[2]}_{6,0}\delta^{[3]}_{6,2}+ a^{[2]}_{7,0}\delta^{[3]}_{7,2} & & a^{[2]}_{1,0}\delta^{[3]}_{1,3} + a^{[2]}_{2,0}\delta^{[3]}_{2,3} + a^{[2]}_{3,0}\delta^{[3]}_{3,3} + a^{[2]}_{4,0}\delta^{[3]}_{4,3} + a^{[2]}_{5,0}\delta^{[3]}_{5,3}+ a^{[2]}_{6,0}\delta^{[3]}_{6,3}+ a^{[2]}_{7,0}\delta^{[3]}_{7,3} \\ a^{[2]}_{1,1}\delta^{[3]}_{1,1} + a^{[2]}_{2,1}\delta^{[3]}_{2,1} + a^{[2]}_{3,1}\delta^{[3]}_{3,1} + a^{[2]}_{4,1}\delta^{[3]}_{4,1} + a^{[2]}_{5,1}\delta^{[3]}_{5,1}+ a^{[2]}_{6,1}\delta^{[3]}_{6,1}+ a^{[2]}_{7,1}\delta^{[3]}_{7,1} & & a^{[2]}_{1,1}\delta^{[3]}_{1,2} + a^{[2]}_{2,1}\delta^{[3]}_{2,2} + a^{[2]}_{3,1}\delta^{[3]}_{3,2} + a^{[2]}_{4,1}\delta^{[3]}_{4,2} + a^{[2]}_{5,1}\delta^{[3]}_{5,2}+ a^{[2]}_{6,1}\delta^{[3]}_{6,2}+ a^{[2]}_{7,1}\delta^{[3]}_{7,2} & & a^{[2]}_{1,1}\delta^{[3]}_{1,3} + a^{[2]}_{2,1}\delta^{[3]}_{2,3} + a^{[2]}_{3,1}\delta^{[3]}_{3,3} + a^{[2]}_{4,1}\delta^{[3]}_{4,3} + a^{[2]}_{5,1}\delta^{[3]}_{5,3}+ a^{[2]}_{6,1}\delta^{[3]}_{6,3}+ a^{[2]}_{7,1}\delta^{[3]}_{7,3} \\ a^{[2]}_{1,2}\delta^{[3]}_{1,1} + a^{[2]}_{2,2}\delta^{[3]}_{2,1} + a^{[2]}_{3,2}\delta^{[3]}_{3,1} + a^{[2]}_{4,2}\delta^{[3]}_{4,1} + a^{[2]}_{5,2}\delta^{[3]}_{5,1}+ a^{[2]}_{6,2}\delta^{[3]}_{6,1}+ a^{[2]}_{7,2}\delta^{[3]}_{7,1} & & a^{[2]}_{1,2}\delta^{[3]}_{1,2} + a^{[2]}_{2,2}\delta^{[3]}_{2,2} + a^{[2]}_{3,2}\delta^{[3]}_{3,2} + a^{[2]}_{4,2}\delta^{[3]}_{4,2} + a^{[2]}_{5,2}\delta^{[3]}_{5,2}+ a^{[2]}_{6,2}\delta^{[3]}_{6,2}+ a^{[2]}_{7,2}\delta^{[3]}_{7,2} & & a^{[2]}_{1,2}\delta^{[3]}_{1,3} + a^{[2]}_{2,2}\delta^{[3]}_{2,3} + a^{[2]}_{3,2}\delta^{[3]}_{3,3} + a^{[2]}_{4,2}\delta^{[3]}_{4,3} + a^{[2]}_{5,2}\delta^{[3]}_{5,3}+ a^{[2]}_{6,2}\delta^{[3]}_{6,3}+ a^{[2]}_{7,2}\delta^{[3]}_{7,3} \\ a^{[2]}_{1,3}\delta^{[3]}_{1,1} + a^{[2]}_{2,3}\delta^{[3]}_{2,1} + a^{[2]}_{3,3}\delta^{[3]}_{3,1} + a^{[2]}_{4,3}\delta^{[3]}_{4,1} + a^{[2]}_{5,3}\delta^{[3]}_{5,1}+ a^{[2]}_{6,3}\delta^{[3]}_{6,1}+ a^{[2]}_{7,3}\delta^{[3]}_{7,1} & & a^{[2]}_{1,3}\delta^{[3]}_{1,2} + a^{[2]}_{2,3}\delta^{[3]}_{2,2} + a^{[2]}_{3,3}\delta^{[3]}_{3,2} + a^{[2]}_{4,3}\delta^{[3]}_{4,2} + a^{[2]}_{5,3}\delta^{[3]}_{5,2}+ a^{[2]}_{6,3}\delta^{[3]}_{6,2}+ a^{[2]}_{7,3}\delta^{[3]}_{7,2} & & a^{[2]}_{1,3}\delta^{[3]}_{1,3} + a^{[2]}_{2,3}\delta^{[3]}_{2,3} + a^{[2]}_{3,3}\delta^{[3]}_{3,3} + a^{[2]}_{4,3}\delta^{[3]}_{4,3} + a^{[2]}_{5,3}\delta^{[3]}_{5,3}+ a^{[2]}_{6,3}\delta^{[3]}_{6,3}+ a^{[2]}_{7,3}\delta^{[3]}_{7,3}\\ a^{[2]}_{1,4}\delta^{[3]}_{1,1} + a^{[2]}_{2,4}\delta^{[3]}_{2,1} + a^{[2]}_{3,4}\delta^{[3]}_{3,1} + a^{[2]}_{4,4}\delta^{[3]}_{4,1} + a^{[2]}_{5,4}\delta^{[3]}_{5,1}+ a^{[2]}_{6,4}\delta^{[3]}_{6,1}+ a^{[2]}_{7,4}\delta^{[3]}_{7,1} & & a^{[2]}_{1,4}\delta^{[3]}_{1,2} + a^{[2]}_{2,4}\delta^{[3]}_{2,2} + a^{[2]}_{3,4}\delta^{[3]}_{3,2} + a^{[2]}_{4,4}\delta^{[3]}_{4,2} + a^{[2]}_{5,4}\delta^{[3]}_{5,2}+ a^{[2]}_{6,4}\delta^{[3]}_{6,2}+ a^{[2]}_{7,4}\delta^{[3]}_{7,2} & & a^{[2]}_{1,4}\delta^{[3]}_{1,3} + a^{[2]}_{2,4}\delta^{[3]}_{2,3} + a^{[2]}_{3,4}\delta^{[3]}_{3,3} + a^{[2]}_{4,4}\delta^{[3]}_{4,3} + a^{[2]}_{5,4}\delta^{[3]}_{5,3}+ a^{[2]}_{6,4}\delta^{[3]}_{6,3}+ a^{[2]}_{7,4}\delta^{[3]}_{7,3} \\ \end{array} \right ) \]
\[ \]
\[ \frac{\partial }{\partial \theta^{[2]}_r} J(\theta) = \left( \begin{array}{J2Condensed} \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{1,1} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{1,2} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{1,3} \\ \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{2,1} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{2,2} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{2,3} \\ \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{3,1} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{3,2} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{3,3} \\ \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{4,1} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{4,2} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{4,3} \\ \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{5,1} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{5,2} & & \frac{\partial }{\partial \theta^{[2]}_r}j(\theta)^{[2]}_{5,3} \\\end{array} \right) \]
\[ \]
\[ \Theta^{[2]} = \Theta^{[2]} - \alpha \frac{\partial }{\partial \theta^{[2]}_r} J(\theta) \\ \]
\[ \]
\[ \Theta^{[2]} = \left( \begin{array}{Theta2} \theta^{[2]}_{0,1} & \theta^{[2]}_{0,2} & \theta^{[2]}_{0,3} \\ \theta^{[2]}_{1,1} & \theta^{[2]}_{1,2} & \theta^{[2]}_{1,3} \\ \theta^{[2]}_{2,1} & \theta^{[2]}_{2,2} & \theta^{[2]}_{2,3} \\ \theta^{[2]}_{3,1} & \theta^{[2]}_{3,2} & \theta^{[2]}_{3,3} \\ \theta^{[2]}_{4,1} & \theta^{[2]}_{4,2} & \theta^{[2]}_{4,3} \\ \end{array} \right)- \alpha \left( \begin{array}{J2Condensed} \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{1,1} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{1,2} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{1,3} \\ \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{2,1} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{2,2} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{2,3} \\ \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{3,1} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{3,2} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{3,3} \\ \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{4,1} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{4,2} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{4,3} \\ \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{5,1} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{5,2} & & \frac{\partial }{\partial \theta^{[2]}_j}j(\theta)^{[2]}_{5,3} \\\end{array} \right) \\ \]
\[ \]
\[ \frac{\partial }{\partial \theta^{[1]}_j} J(\theta) = ( A^{[1]} )^{T} \cdot \delta^{[2]} = \left( \begin{array}{A1} a^{[1]}_{1,0} & a^{[1]}_{1,1} & a^{[1]}_{1,2} & a^{[1]}_{1,3} \\ a^{[1]}_{2,0} & a^{[1]}_{2,1} & a^{[1]}_{2,2} & a^{[1]}_{2,3} \\ a^{[1]}_{3,0} & a^{[1]}_{3,1} & a^{[1]}_{3,2} & a^{[1]}_{3,3} \\ a^{[1]}_{4,0} & a^{[1]}_{4,1} & a^{[1]}_{4,2} & a^{[1]}_{4,3} \\ a^{[1]}_{5,0} & a^{[1]}_{5,1} & a^{[1]}_{5,2} & a^{[1]}_{5,3} \\ a^{[1]}_{6,0} & a^{[1]}_{6,1} & a^{[1]}_{6,2} & a^{[1]}_{6,3} \\ a^{[1]}_{7,0} & a^{[1]}_{7,1} & a^{[1]}_{7,2} & a^{[1]}_{7,3} \\ \end{array} \right) ^{T} \cdot \left( \begin{array}{delta2} \delta^{[2]}_{1,1} & \delta^{[2]}_{1,2} & \delta^{[2]}_{1,3} & \delta^{[2]}_{1,4} & \delta^{[2]}_{1,5} \\ \delta^{[2]}_{2,1} & \delta^{[2]}_{2,2} & \delta^{[2]}_{2,3} & \delta^{[2]}_{2,4} & \delta^{[2]}_{2,5} \\ \delta^{[2]}_{3,1} & \delta^{[2]}_{3,2} & \delta^{[2]}_{3,3} & \delta^{[2]}_{3,4} & \delta^{[2]}_{3,5} \\ \delta^{[2]}_{4,1} & \delta^{[2]}_{4,2} & \delta^{[2]}_{4,3} & \delta^{[2]}_{4,4} & \delta^{[2]}_{4,5} \\ \delta^{[2]}_{5,1} & \delta^{[2]}_{5,2} & \delta^{[2]}_{5,3} & \delta^{[2]}_{5,4} & \delta^{[2]}_{5,5} \\ \delta^{[2]}_{6,1} & \delta^{[2]}_{6,2} & \delta^{[2]}_{6,3} & \delta^{[2]}_{6,4} & \delta^{[2]}_{6,5} \\ \delta^{[2]}_{7,1} & \delta^{[2]}_{7,2} & \delta^{[2]}_{7,3} & \delta^{[2]}_{7,4} & \delta^{[2]}_{7,5} \\ \end{array} \right ) \]
\[ \]
\[ \color{gray} \left\vert{\Theta^{[1]}}\right\vert = \{ u^{[1]} \times (u^{[2]}+1) \} \]
\[ \]
##
## ========================================================================
## ANNBackPropagation.r
## ========================================================================
ANNBackPropagation <- function(numHiddenLayers) {
for (layerCount in (numHiddenLayers + 1):1) {
Theta <- get(paste("Theta", layerCount, sep = ""))
delta <- get(paste("delta", (layerCount + 1), sep = ""))
a <- get(paste("a", layerCount, sep = ""))
newDelta <- t(t(matrix(Theta[, -1], ncol = (dim(Theta)[2] - 1))) %*%
t(delta)) * (a[, -1] * (1 - a[, -1]))
# newDelta<-t(t(Theta[,-1])%*%t(delta))*(a[,-1]*(1-a[,-1]))
assign(paste("delta", layerCount, sep = ""), newDelta)
}
for (layerCount in (numHiddenLayers + 1):1) {
delta <- get(paste("delta", (layerCount + 1), sep = ""))
a <- get(paste("a", layerCount, sep = ""))
newGradient <- (t(a[, -1]) %*% as.matrix(delta))
assign(paste("gradient", layerCount, sep = ""), newGradient)
}
m <- dim(a)[1]
for (layerCount in (numHiddenLayers + 1):1) {
Theta <- get(paste("Theta", layerCount, sep = ""))
gradient <- get(paste("gradient", layerCount, sep = ""))
## A bias term is taken into account in the following by excluding column
## one (i.e. 'seq(2,dim(Theta)[2])')
newTheta <- Theta[, seq(2, dim(Theta)[2])] - t((alpha/m) * gradient) +
(lambda/m) * Theta[, seq(2, dim(Theta)[2])]
assign(paste("Theta", layerCount, sep = ""), newTheta)
}
Thetas <- c(dim(Theta1), Theta1)
for (layerCount in 2:(numHiddenLayers + 1)) {
Thetas <- c(Thetas, dim(get(paste("Theta", layerCount, sep = ""))),
get(paste("Theta", layerCount, sep = "")))
}
return(Thetas)
}